- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к учебному занятию по математике на тему Основные методы решения уравнений
Содержание
- 1. Презентация к учебному занятию по математике на тему Основные методы решения уравнений
- 2. СИСТЕМА ОЦЕНИВАНИЯДля каждой группы
- 3. Слайд 3
- 4. Слайд 4
- 5. « Уравнения – это золотой ключ, открывающий
- 6. Основные методы решения уравнений
- 7. Цели занятия:Повторить какие методы решения уравнений нам
- 8. Метод разложения на множителиВыполнила студентка группы 2/6Кравченко Анастасия
- 9. Теория Уравнениеf(x)g(x)h(x)=0можно записать совокупностью уравненийf(x)=0, g(x)=0, h(x)=0.Выбираем те корни, которые принадлежат области определения исходного уравнения.
- 10. Решение примера (
- 11. Интернет ресурсыhttp://images.yandex.ru/http://reshuege.ru/testhttp://math.semestr.ru/math/factor.phphttp://www.fxyz.ru/
- 12. Введение новой переменной Работу выполнилаСтудентка группы 2/6Гончарова Дарья
- 13. С методом введения новой переменной при решении рациональных
- 14. Если уравнение у=f(x) преобразовали к виду p(g(x))=0,
- 15. ПРИМЕРЫ:Пример 2. Решить уравнение.х4 – 17х² +
- 16. · http://school.xvatit.com/index.php?title=Методы_решения_систем_уравнений · http://mmosysert.ucoz.ru/evrika/glavatskix/proekt.pdf · http://referatplus.ru/matematika_geometriya/1_matemat_new_0040.php · http://www.coolmath.ru/lessons/8/436-raczionalnye-uravneniya.html · http://5klass.net/algebra-8-klass/Vidy-kvadratnykh-uravnenij/015-Vvedenie-novoj-peremennoj.html ИСТОЧНИКИ:
- 17. Функционально-графический метод решения уравненийРаботу выполниластудентка группы 2/6Воробьева Евгения
- 18. Алгоритм решенияУравнение f(x)=g(x)1)Построить графики функцийy=f(x) , y=g(x);2)Найти
- 19. Примеры решений:1)Строим y= x², y = -6x-8;2)Находим
- 20. 1)Строим графикифункций y=(х+1) ; y= 2;
- 21. Источники:http://images.yandex.ru/http://ppt4web.ru/algebra/graficheskijj-sposob-reshenija-uravnenijj0.htmlhttp://ru.convdocs.org/docs/index-99946.html?page=2
- 22. Замена уравненияh(f(x)) = h(g(x))уравнениемf(x)=g(x)
- 23. При решении показательных уравненийaf(x)=ag(x) (a>0,
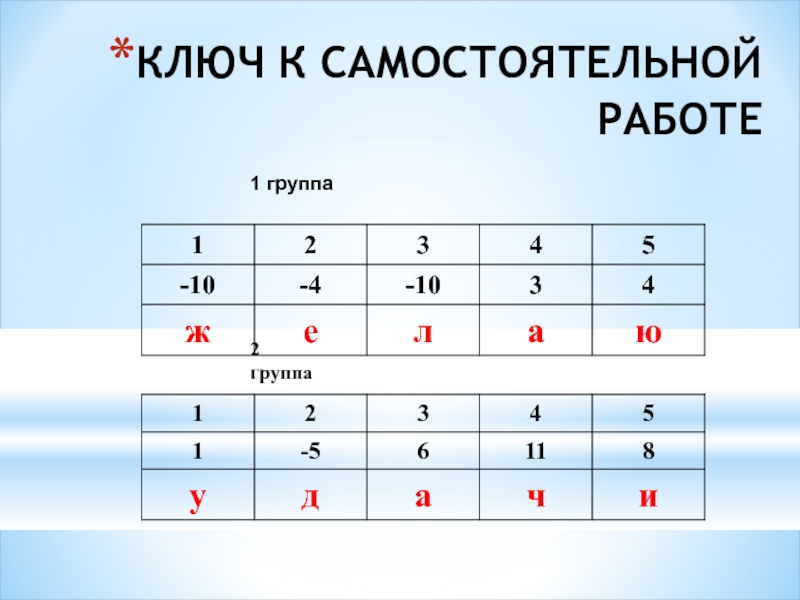
- 24. КЛЮЧ К САМОСТОЯТЕЛЬНОЙ РАБОТЕ2 группа1 группа
- 25. Укажи метод решения уравнения
- 26. «Метод решения хорош, если с
- 27. Цели занятия:Повторить какие методы решения уравнений нам
- 28. « Уравнения – это золотой ключ, открывающий
- 29. СИСТЕМА ОЦЕНИВАНИЯДля каждой группы
- 30. БУКЕТ НАСТРОЕНИЯ
- 31. Красный – вы стремитесь к лидерству, вам
- 32. Спасибо за работу!
Слайд 7Цели занятия:
Повторить какие методы решения уравнений нам известны.
Выделить основные методы решения
Учиться применять их при решении уравнений разного типа
Проверить насколько хорошо мы ими владеем.
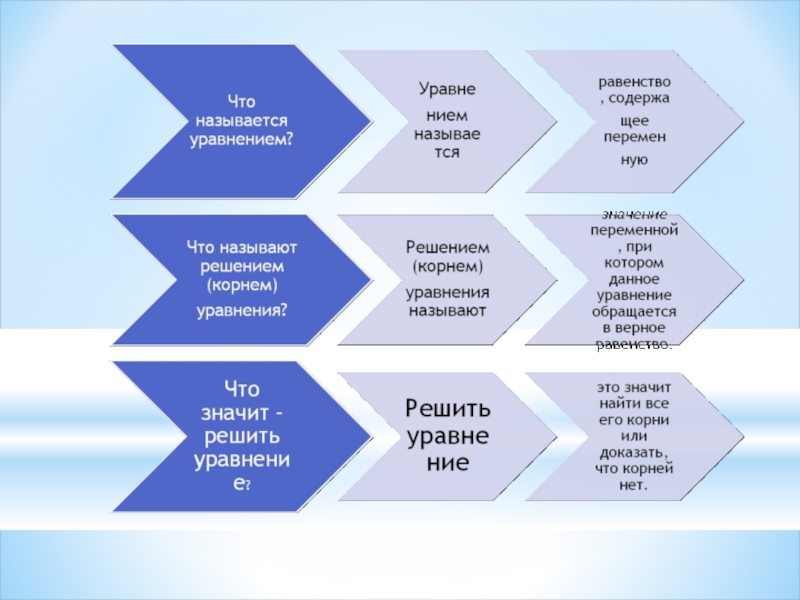
Слайд 9 Теория
Уравнение
f(x)g(x)h(x)=0
можно записать совокупностью уравнений
f(x)=0, g(x)=0, h(x)=0.
Выбираем те корни, которые
Слайд 10Решение примера
( -3) In(х-8)=0
=3 х-8=1 х+2 >0
Х+2=9 х=9 х-8 >0
Х=7
С учетом ОДЗ: х=9
Ответ: 9
Слайд 11Интернет ресурсы
http://images.yandex.ru/
http://reshuege.ru/test
http://math.semestr.ru/math/factor.php
http://www.fxyz.ru/
Слайд 13С методом введения новой переменной при решении рациональных уравнений с одной переменной
Слайд 14Если уравнение у=f(x) преобразовали к виду p(g(x))=0, то нужно ввести новую
g(u)=u1 ; g(u)=u2 ;…,g(u)=un где u1, …,un корни p(u)=0
При решении различных видов уравнений: рациональных,
тригонометрических, показательных часто используется метод введения новой переменной.
Новая переменная в уравнениях иногда действительно
очевидна, но иногда ее трудно увидеть, а можно выявить только лишь в процессе каких либо преобразований.
Бывает полезно ввести не одну, а две переменные.
2 sin2 x + 13 sin x + 11 = 0
Слайд 15ПРИМЕРЫ:
Пример 2. Решить уравнение.
х4 – 17х² + 16 = 0
х4 =
t² - 17t +16 = 0
t1 = 16 t2 = 1
х² = 16 и х² = 1
x1,2 = ± 4 и х3,4 = ± 1
Ответ: ± 4; ± 1
Слайд 16· http://school.xvatit.com/index.php?title=Методы_решения_систем_уравнений
· http://mmosysert.ucoz.ru/evrika/glavatskix/proekt.pdf
· http://referatplus.ru/matematika_geometriya/1_matemat_new_0040.php
· http://www.coolmath.ru/lessons/8/436-raczionalnye-uravneniya.html
· http://5klass.net/algebra-8-klass/Vidy-kvadratnykh-uravnenij/015-Vvedenie-novoj-peremennoj.html
ИСТОЧНИКИ:
Слайд 17Функционально-графический метод решения уравнений
Работу выполнила
студентка группы 2/6
Воробьева Евгения
Слайд 18Алгоритм решения
Уравнение f(x)=g(x)
1)Построить графики функций
y=f(x) , y=g(x);
2)Найти координаты точек их пересечения;
3)Определить
4)Записать ответ (в ответе указываются значения пункта 3).
Если, например одна из функций y=f(x) , y=g(x) возрастает, а другая убывает, то уравнение f(x)=g(x) либо не имеет корней, либо имеет один корень, который можно найти путём подбора.
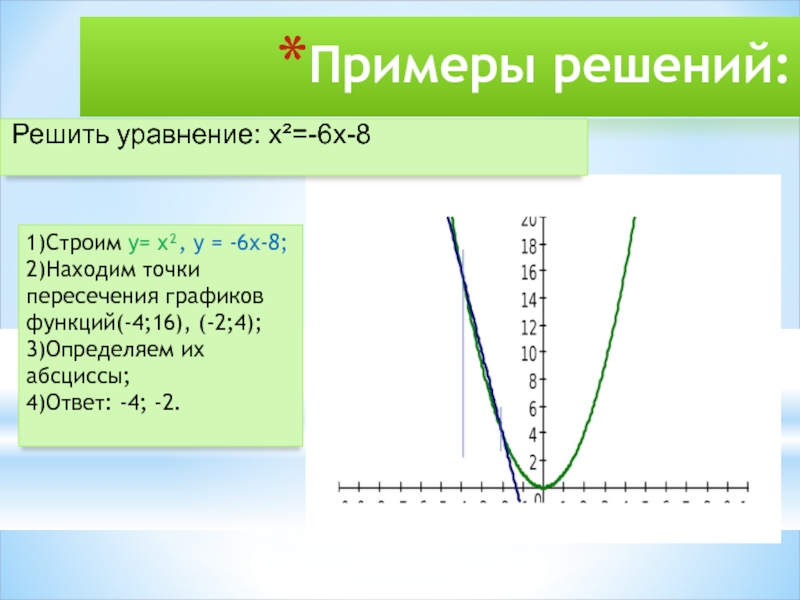
Слайд 19Примеры решений:
1)Строим y= x², y = -6x-8;
2)Находим точки пересечения графиков функций(-4;16),
3)Определяем их абсциссы;
4)Ответ: -4; -2.
Решить уравнение: x²=-6x-8
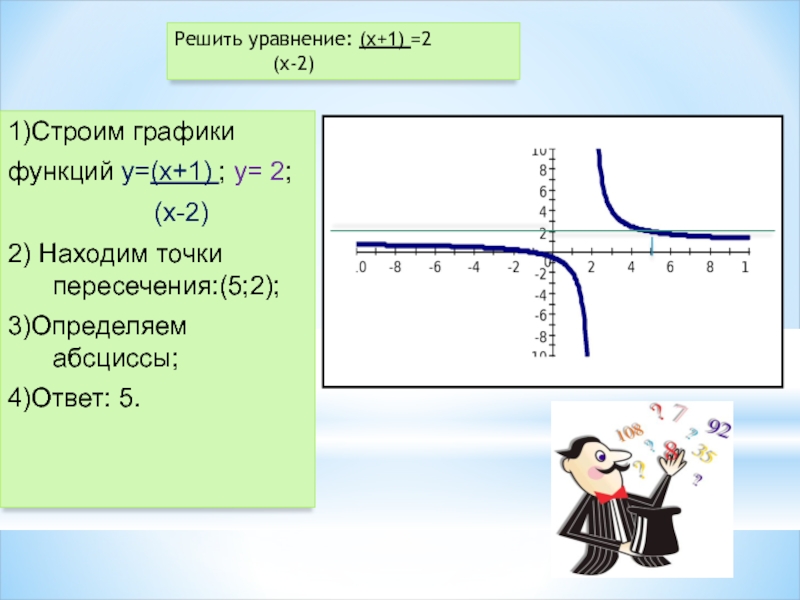
Слайд 201)Строим графики
функций y=(х+1) ; y= 2;
2) Находим точки пересечения:(5;2);
3)Определяем абсциссы;
4)Ответ: 5.
Решить уравнение: (х+1) =2
(х-2)
Слайд 21Источники:
http://images.yandex.ru/
http://ppt4web.ru/algebra/graficheskijj-sposob-reshenija-uravnenijj0.html
http://ru.convdocs.org/docs/index-99946.html?page=2
Слайд 23При решении показательных уравнений
af(x)=ag(x) (a>0, a≠1) f(x)=g(x)
При решении
logaf(x) = logag(x) f(x) = g(x)
При решении иррациональных уравнений
f(x) = g(x)
Этот метод можно применять
только тогда, когда y=h(x) –
монотонная функция.
Слайд 26 «Метод решения хорош, если с самого начала мы можем
Лейбниц.
ЛЕЙБНИЦ (Leibniz) Готфрид Вильгельм (1646-1716), немецкий философ, математик, физик, языковед. Основатель и президент (с 1700) Бранденбургского научного общества (позднее – Берлинская АН). По просьбе Петра I разработал проекты развития образования и государственного управления в России.
Слайд 27Цели занятия:
Повторить какие методы решения уравнений нам известны.
Выделить основные методы решения
Учиться применять их при решении уравнений разного типа
Проверить насколько хорошо мы ими владеем.
Слайд 31
Красный – вы стремитесь к лидерству, вам не хватает новых завоеваний
Оранжевый – знак возбуждения нервной системы. Это значит, что вы созрели для каких-то серьезных перемен в жизни.
Синий – вам нужна сильная разрядка и полноценный отдых.
Зеленый – символизирует потребность в самоутверждении, тягу к знаниям или желание карьерного роста.
Голубой – мечтаете о чем-то романтическом, возвышенном, далеком. Вы хотите быть максимально открытым, правдивым.
Жёлтый-оптимизм переполняет Вашу душу и заставляет сердце стучать быстрее. Вы расслаблены и полны мечтами об удаче.
Розовый – вам не хватает нежности и легкости. Вероятно, вы немного устали от серьезной работы, четких планов, вас тянет к чему-нибудь беззаботному.