Богачева Нина Владимировна
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Мастер-класс по теме Производная функции.
Содержание
- 1. Мастер-класс по теме Производная функции.
- 2. Цели мастер – класса:Обучающая: обобщить и систематизировать
- 3. Технологии: индивидуально–дифференцированного обучения, ИКТ.Методы обучения: словесный, наглядный,
- 4. Структура мастер – класса:I.Организационный момент -1 мин.II.Сообщение
- 5. Ход мастер – класса: I.Организационный момент.II.Сообщение темы,
- 6. Вы овладели теоретическими знаниями по теме «Производная».
- 7. Подведем итог. Какова была цель урока? Как
- 8. Приложение 1Задача 1 (о скорости движения).По прямой,
- 9. Решение задач:Фиксируем момент t, в который
- 10. Прямая, проходящая через точку М0 (х0; f(х0)),
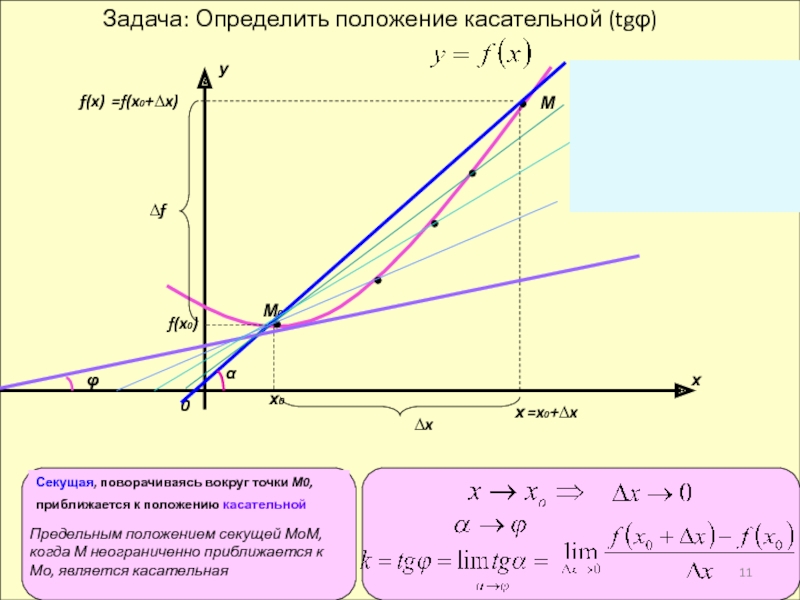
- 11. Задача: Определить положение касательной (tgφ)ху0М0х0f(x0)Мхf(x)=x0+∆x∆x∆f=f(x0+∆x)φСекущая, поворачиваясь вокруг
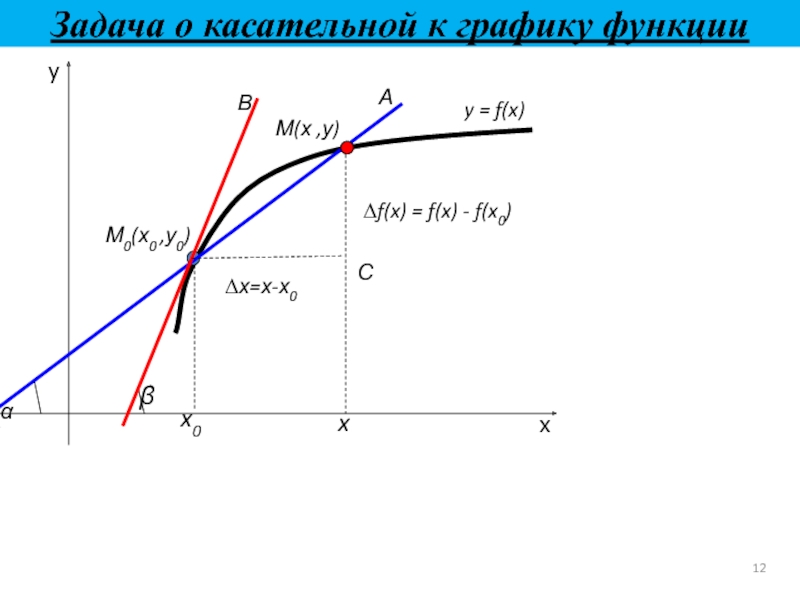
- 12. Задача о касательной к графику функцииxyС∆х=х-х0∆f(x) = f(x) - f(x0)
- 13. Задача о мгновенной величине токаОбозначим через q
- 14. ВыводыРазличные задачи привели в процессе решения к
- 15. Задача о скорости химической реакцииСредняя скорость растворения
- 16. Определение производнойПроизводной функции f в точке х0
- 17. Возвращаясь к рассмотренным задачам, важно подчеркнуть следующее:а)
- 18. А л г о р и т
- 19. А это значит:Аппарат производной можно использовать при
- 20. Основные формулыСредняя скорость
- 21. Приложение 2 Задачи 7 ЕГЭЗадача 1Материальная точка
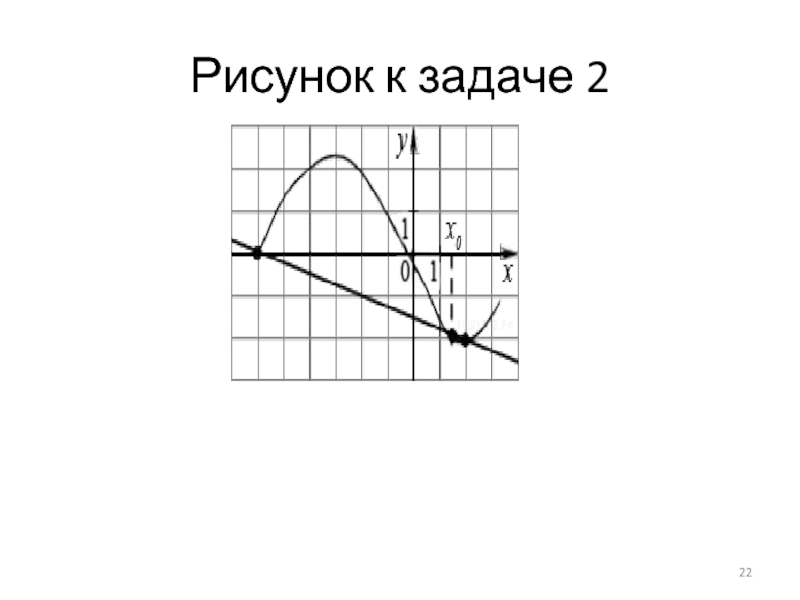
- 22. Рисунок к задаче 2 .
- 23. Задача 3 На рисунке изображен график производной функции
- 24. Задача 4 На рисунке изображён график
- 25. Приложение 31 пара№1 Найдите точку минимума функции
- 26. Приложение 4 Тест1. Напишите уравнение касательной
- 27. Спасибо за внимание!!!
Цели мастер – класса:Обучающая: обобщить и систематизировать знания учащихся по теме «Производная функции”, рассмотреть прототипы задач ЕГЭ по данной теме, вести подготовку к итоговой аттестации;предоставить обучающимся возможность проверить свои знания при самостоятельном решении задач.Развивающая: способствовать развитию
Слайд 1Мастер – класс по теме:
«Производная функции».
Подготовила учитель математики МКОУ Русскогвоздевская СОШ
Слайд 2Цели мастер – класса:
Обучающая: обобщить и систематизировать знания учащихся по теме
«Производная функции”,
рассмотреть прототипы задач ЕГЭ по данной теме, вести подготовку к итоговой аттестации;
предоставить обучающимся возможность проверить свои знания при самостоятельном решении задач.
Развивающая: способствовать развитию памяти, внимания, навыков самооценки и самоконтроля;
формированию таких ключевых компетенций, как сравнение, сопоставление, классификация объектов,
определение адекватных способов решения учебной задачи на основе заданных алгоритмов,
способность самостоятельно действовать в ситуации неопределённости, контролировать и оценивать
свою деятельность, находить и устранять причины возникших трудностей.
Воспитательная: развивать у обучающихся коммуникативные компетенции (культуру общения, умение
работать в парах); способствовать воспитанию воли и упорства для достижения конечных результатов.
Слайд 3Технологии: индивидуально–дифференцированного обучения, ИКТ.
Методы обучения: словесный, наглядный, практический, проблемный.
Формы работы: индивидуальная,
фронтальная, в парах.
Оборудование и материалы для урока: проектор, экран, презентация к уроку, индивидуально – дифференцированные карточки для самостоятельной работы в парах ,список сайтов сети Интернет, индивидуально-дифференцированное домашнее задание, интерактивный тест.
Пояснение к уроку. Данный мастер – класс проводится в 11 классе с целью подготовки к ЕГЭ. Нацелен на обобщение теоретического материала по теме «Производная функции» и применение его при решении экзаменационных задач.
Продолжительность мастер – класса – 30 мин.
Оборудование и материалы для урока: проектор, экран, презентация к уроку, индивидуально – дифференцированные карточки для самостоятельной работы в парах ,список сайтов сети Интернет, индивидуально-дифференцированное домашнее задание, интерактивный тест.
Пояснение к уроку. Данный мастер – класс проводится в 11 классе с целью подготовки к ЕГЭ. Нацелен на обобщение теоретического материала по теме «Производная функции» и применение его при решении экзаменационных задач.
Продолжительность мастер – класса – 30 мин.
Слайд 4Структура мастер – класса:
I.Организационный момент -1 мин.
II.Сообщение темы, цели мастер -
класса, мотивация учебной деятельности-1 мин.
III. Показ презентации по теме: “Производная, и ее применение ”(Приложение 1).
III. Тренинг «Задания 8 ЕГЭ». Анализ работы с тренажёром - 6 мин.
IV.Индивидуально - дифференцированная работа в парах. Самостоятельное решение задач 12. Взаимопроверка - 7 мин.
V.Проверка индивидуального задания. -3 мин.
VI. Тестирование. Анализ результатов тестирования -9 мин.
VII. Индивидуально – дифференцированное домашнее задание -1 мин.
VIII.Оценки за урок - 1 мин.
IX.Рефлексия -1 мин.
III. Показ презентации по теме: “Производная, и ее применение ”(Приложение 1).
III. Тренинг «Задания 8 ЕГЭ». Анализ работы с тренажёром - 6 мин.
IV.Индивидуально - дифференцированная работа в парах. Самостоятельное решение задач 12. Взаимопроверка - 7 мин.
V.Проверка индивидуального задания. -3 мин.
VI. Тестирование. Анализ результатов тестирования -9 мин.
VII. Индивидуально – дифференцированное домашнее задание -1 мин.
VIII.Оценки за урок - 1 мин.
IX.Рефлексия -1 мин.
Слайд 5Ход мастер – класса:
I.Организационный момент.
II.Сообщение темы, целей мастер - класса, мотивация
учебной деятельности.
III.Презентация по теме: “Производная, и ее применение”.(Приложение 1)
Посмотрев, презентацию, мы выяснили, какие знания и умения о функции и её производной нужны для успешного решения задач по теме «Производная»:
ЗНАТЬ
правила вычисления производных;
производные основных элементарных функций;
геометрический и физический смысл производной; уравнение касательной к графику функции; исследование функции с помощью производной.
УМЕТЬ
выполнять действия с функциями (описывать по графику поведение и свойства функции, находить её наибольшее и наименьшее значения).
ИСПОЛЬЗОВАТЬ
приобретенные знания и умения в практической деятельности и повседневной жизни.
III.Презентация по теме: “Производная, и ее применение”.(Приложение 1)
Посмотрев, презентацию, мы выяснили, какие знания и умения о функции и её производной нужны для успешного решения задач по теме «Производная»:
ЗНАТЬ
правила вычисления производных;
производные основных элементарных функций;
геометрический и физический смысл производной; уравнение касательной к графику функции; исследование функции с помощью производной.
УМЕТЬ
выполнять действия с функциями (описывать по графику поведение и свойства функции, находить её наибольшее и наименьшее значения).
ИСПОЛЬЗОВАТЬ
приобретенные знания и умения в практической деятельности и повседневной жизни.
Слайд 6Вы овладели теоретическими знаниями по теме «Производная». Сегодня мы будем учиться
применять знания о производной для решения задач ЕГЭ.
Недаром Аристотель говорил, что
“УМ ЗАКЛЮЧАЕТСЯ НЕ ТОЛЬКО В ЗНАНИИ, НО И В УМЕНИИ ПРИМЕНЯТЬ ЗНАНИЯ НА ПРАКТИКЕ”
В конце урока мы вернёмся к цели нашего урока и выясним, достигли ли её?
Применим теоретические знания для решения практических задач.
IV. Тренинг «Задания 8 ЕГЭ». Анализ работы - 6 мин. ( Приложение 2).
V.Индивидуально - дифференцированная работа в парах. Самостоятельное решение задач 12. Взаимопроверка - 7 мин. (Приложение 3).
VI. Тестирование. Анализ результатов тестирования -9 мин. ( Приложение 4).
VII. Индивидуально – дифференцированное домашнее задание -1 мин.
Составить тест по теме “Применение производной”. Задания могут быть с выбором ответа или с кратким ответом, например:
Найти производную
Найти точки максимума или минимума
Найти промежутки возрастания или убывания
Найти наибольшее значение функции и т.д.
VIII.Оценки за урок - 1 мин.
IX.Рефлексия -1 мин.
Недаром Аристотель говорил, что
“УМ ЗАКЛЮЧАЕТСЯ НЕ ТОЛЬКО В ЗНАНИИ, НО И В УМЕНИИ ПРИМЕНЯТЬ ЗНАНИЯ НА ПРАКТИКЕ”
В конце урока мы вернёмся к цели нашего урока и выясним, достигли ли её?
Применим теоретические знания для решения практических задач.
IV. Тренинг «Задания 8 ЕГЭ». Анализ работы - 6 мин. ( Приложение 2).
V.Индивидуально - дифференцированная работа в парах. Самостоятельное решение задач 12. Взаимопроверка - 7 мин. (Приложение 3).
VI. Тестирование. Анализ результатов тестирования -9 мин. ( Приложение 4).
VII. Индивидуально – дифференцированное домашнее задание -1 мин.
Составить тест по теме “Применение производной”. Задания могут быть с выбором ответа или с кратким ответом, например:
Найти производную
Найти точки максимума или минимума
Найти промежутки возрастания или убывания
Найти наибольшее значение функции и т.д.
VIII.Оценки за урок - 1 мин.
IX.Рефлексия -1 мин.
Слайд 7Подведем итог. Какова была цель урока? Как вы считаете, достигнута ли
она?
Посмотрите на доску и одним предложением, выбирая начало фразы, продолжите предложение, которое вам больше всего подходит.
Я почувствовал…
Я научился…
У меня получилось …
Я смог…
Я попробую …
Меня удивило, что …
Мне захотелось…
А закончить урок я хотела бы словами итальянского
философа Фомы Аквинского
«Знание – столь драгоценная вещь, что его не зазорно добывать из любого источника»
Желаю успехов в подготовке к ЕГЭ!
Посмотрите на доску и одним предложением, выбирая начало фразы, продолжите предложение, которое вам больше всего подходит.
Я почувствовал…
Я научился…
У меня получилось …
Я смог…
Я попробую …
Меня удивило, что …
Мне захотелось…
А закончить урок я хотела бы словами итальянского
философа Фомы Аквинского
«Знание – столь драгоценная вещь, что его не зазорно добывать из любого источника»
Желаю успехов в подготовке к ЕГЭ!
Слайд 8Приложение 1
Задача 1 (о скорости движения).
По прямой, на которой заданы начало
отсчета, единица измерения (метр) и направление, движется некоторое тело (материальная точка).
Закон движения задан формулой s=s (t), где t — время (в секундах), s (t) — положение тела на прямой (координата движущейся материальной
точки) в момент времени t по отношению к началу отсчета (в метрах).
Найти скорость движения тела в момент времени t (в м/с).
Задача 2 (о бросании камня)
Поднимем камешек и затем из состояния покоя отпустим его. Движение
свободно падающего тела явно неравномерное. Скорость v постепенно
возрастает. Но как именно выглядит зависимость v(t) ?
Закон движения задан формулой s=s (t), где t — время (в секундах), s (t) — положение тела на прямой (координата движущейся материальной
точки) в момент времени t по отношению к началу отсчета (в метрах).
Найти скорость движения тела в момент времени t (в м/с).
Задача 2 (о бросании камня)
Поднимем камешек и затем из состояния покоя отпустим его. Движение
свободно падающего тела явно неравномерное. Скорость v постепенно
возрастает. Но как именно выглядит зависимость v(t) ?
Слайд 9 Решение задач:
Фиксируем момент t, в который мы хотим знать значение
скорости v(t). Пусть h – небольшой промежуток времени, прошедший от момента t. За это время падающее тело пройдёт путь, равный s(t+h)-s(t).
Если промежуток времени h очень мал, то приближённо
s(t+h)-s(t)≈v(t)∙h, или , причём
последнее приближённое равенство тем точнее, чем меньше h. Значит величину v(t) скорости в момент t можно рассматривать как предел, к которому стремится отношение, выражающее среднюю скорость на интервале времени от момента t до момента t+h. Сказанное записывают в виде
Если промежуток времени h очень мал, то приближённо
s(t+h)-s(t)≈v(t)∙h, или , причём
последнее приближённое равенство тем точнее, чем меньше h. Значит величину v(t) скорости в момент t можно рассматривать как предел, к которому стремится отношение, выражающее среднюю скорость на интервале времени от момента t до момента t+h. Сказанное записывают в виде
Слайд 10Прямая, проходящая через точку М0 (х0; f(х0)), с отрезком которой почти
сливается график функции f(х),называют касательной к графику в точке х0
x0
f(x0)
M0
X
y
Задача, приводящая к понятию “производной”
0
Слайд 11Задача: Определить положение касательной (tgφ)
х
у
0
М0
х0
f(x0)
М
х
f(x)
=x0+∆x
∆x
∆f
=f(x0+∆x)
φ
Секущая, поворачиваясь вокруг точки М0,
приближается к
положению касательной
Предельным положением секущей МоМ,
когда М неограниченно приближается к Мо, является касательная
Слайд 13Задача о мгновенной величине тока
Обозначим через q = q(t) количество электричества,
протекающее через поперечное сечение проводника за время t.
Пусть Δt – некоторый промежуток времени, Δq = q(t+Δt) – q(t) – количество электричества, протекающее через указанное сечение за промежуток времени от момента t до момента t + Δt. Тогда отношение называют средней силой тока.
Мгновенной силой тока в момент времени t называется предел отношения приращения количества электричества Δq ко времени Δt, при условии, что Δt→0.
Пусть Δt – некоторый промежуток времени, Δq = q(t+Δt) – q(t) – количество электричества, протекающее через указанное сечение за промежуток времени от момента t до момента t + Δt. Тогда отношение называют средней силой тока.
Мгновенной силой тока в момент времени t называется предел отношения приращения количества электричества Δq ко времени Δt, при условии, что Δt→0.
Слайд 14Выводы
Различные задачи привели в процессе решения к одной и той же
математической модели – пределу отношения приращения функции к приращению аргумента при условии, что приращение аргумента стремится к нулю. Значит, эту математическую модель надо специально изучить, т.е.:
Присвоить ей новый термин.
Ввести для неё обозначение.
Исследовать свойства новой модели.
Определить возможности применения нового понятия - производная
Присвоить ей новый термин.
Ввести для неё обозначение.
Исследовать свойства новой модели.
Определить возможности применения нового понятия - производная
Слайд 15Задача о скорости химической реакции
Средняя скорость растворения соли в воде за
промежуток времени [t0;t1] (масса соли, растворившейся в воде изменяется по закону х = f(t)) определяется по формуле .
Скорость растворения в данный
момент времени
Скорость растворения в данный
момент времени
Слайд 16Определение производной
Производной функции f в точке х0 называется предел отношения приращения
функции к приращению аргумента при последнем стремящимся к нулю:
Слайд 17Возвращаясь к рассмотренным задачам, важно подчеркнуть следующее:
а) мгновенная скорость неравномерного движения
есть производная от пути по времени;
б) угловой коэффициент касательной к графику функции в точке (x0; f(x)) есть производная функции f(x) в точке х = х0;
в) мгновенная сила тока I(t) в момент t есть производная от количества электричества q(t) по времени;
Г) скорость химической реакции в данный момент времени t есть производная от количества вещества у(t), участвующего в реакции, по времени t.
б) угловой коэффициент касательной к графику функции в точке (x0; f(x)) есть производная функции f(x) в точке х = х0;
в) мгновенная сила тока I(t) в момент t есть производная от количества электричества q(t) по времени;
Г) скорость химической реакции в данный момент времени t есть производная от количества вещества у(t), участвующего в реакции, по времени t.
Слайд 19А это значит:
Аппарат производной можно использовать при решении геометрических задач, задач
из естественных и гуманитарных наук, экономических задач оптимизационного характера.
И, конечно, не обойтись без производной при исследовании функции и построении графиков, решении уравнений и неравенств
И, конечно, не обойтись без производной при исследовании функции и построении графиков, решении уравнений и неравенств
«…нет ни одной области в математике, которая когда-либо не окажется применимой к явлениям действительного мира…» Н.И. Лобачевский
Слайд 20Основные формулы
Средняя скорость
=
Мгновенная скорость
или
Скорость изменения функции
Значение производной в точке
= k
Мгновенная скорость
или
Скорость изменения функции
Значение производной в точке
= k
Слайд 21Приложение 2
Задачи 7 ЕГЭ
Задача 1
Материальная точка движется прямолинейно по закону
x(t)=6t^2-48t+17 (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). Найдите ее скорость (в м/с) в момент времени t = 9 с.
Ответ: 60.
Задача 2
На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0. Рис.1
Ответ: − 0,25.
Ответ: 60.
Задача 2
На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0. Рис.1
Ответ: − 0,25.
Слайд 23Задача 3 На рисунке изображен график производной функции f(x) , определенной на интервале
(-6,6) . Найдите промежутки возрастания функции f(x). В ответе укажите сумму целых точек, входящих в эти промежутки.
Ответ:14
Слайд 24Задача 4 На рисунке изображён график функции y = F(x) — одной из первобразных
функции f(x), определённой на интервале (−3; 5). Найдите количество решений уравнения f(x)=0 на отрезке [−2; 4].
Ответ: 10
Слайд 25Приложение 3
1 пара
№1 Найдите точку минимума функции
у =10х-ln(х+9)+6
№2 Найдите наименьшее значение функции y=x^3-27x на отрезке [0;4].
2 пара
№1 Найдите наименьшее значение функции у=(х-10) на отрезке [8; 10] .
№2 Найти точку максимума функции у= x^3-3x^2+2.
Слайд 26Приложение 4
Тест
1. Напишите уравнение касательной к графику функции f(x)=3x^4+6x^2-9x-x^3 в точке
x=2 .
1)у = – 87х – 136 3) у = 87х – 136
2)у = – 88х + 142 4) у = 85х + 142
2. Прямолинейное движение точки описывается законом x(t)=t^4-3t . Найдите ускорение в момент времени t = 1.
1) 4 2) 1 3) 24 4) 12
3. Найдите длину промежутка возрастания функции y=-2x^3+3x^2+36x+1 .
1) 2 2) 1 3) 5 4) 6
Ответы на тест:1.-3, 2-4,3-3.
1)у = – 87х – 136 3) у = 87х – 136
2)у = – 88х + 142 4) у = 85х + 142
2. Прямолинейное движение точки описывается законом x(t)=t^4-3t . Найдите ускорение в момент времени t = 1.
1) 4 2) 1 3) 24 4) 12
3. Найдите длину промежутка возрастания функции y=-2x^3+3x^2+36x+1 .
1) 2 2) 1 3) 5 4) 6
Ответы на тест:1.-3, 2-4,3-3.












![Мастер-класс по теме Производная функции. Задача о скорости химической реакцииСредняя скорость растворения соли в воде за Задача о скорости химической реакцииСредняя скорость растворения соли в воде за промежуток времени [t0;t1] (масса соли, растворившейся](/img/thumbs/329ad2577c5f073a9cbe4ddba2e48358-800x.jpg)