- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Графики функций 9кл
Содержание
- 1. Графики функций 9кл
- 2. Линейнаяy=kxпрямая
- 3. коэффициент пропорциональности. На рисунке пример для k = 1,
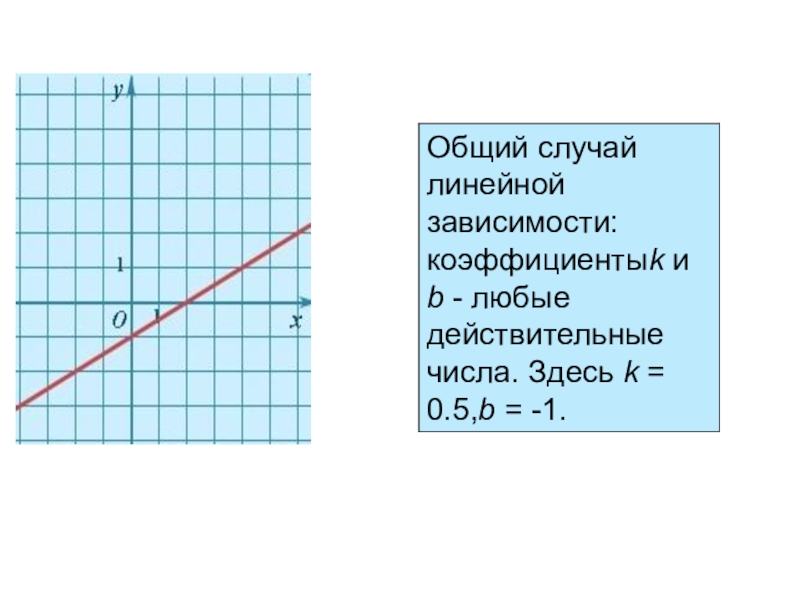
- 4. Линейнаяy=kx+bпрямая
- 5. Слайд 5
- 6. КвКвадратичнаяy=х² парабола
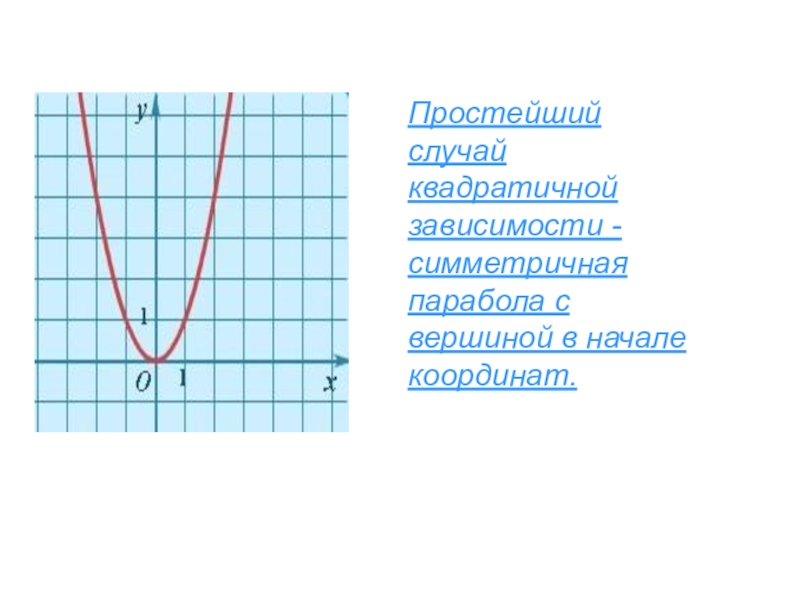
- 7. Простейший случай квадратичной зависимости - симметричная парабола с вершиной в начале координат.
- 8. Квадратичнаяпараболаy = ax2 + bx+ c
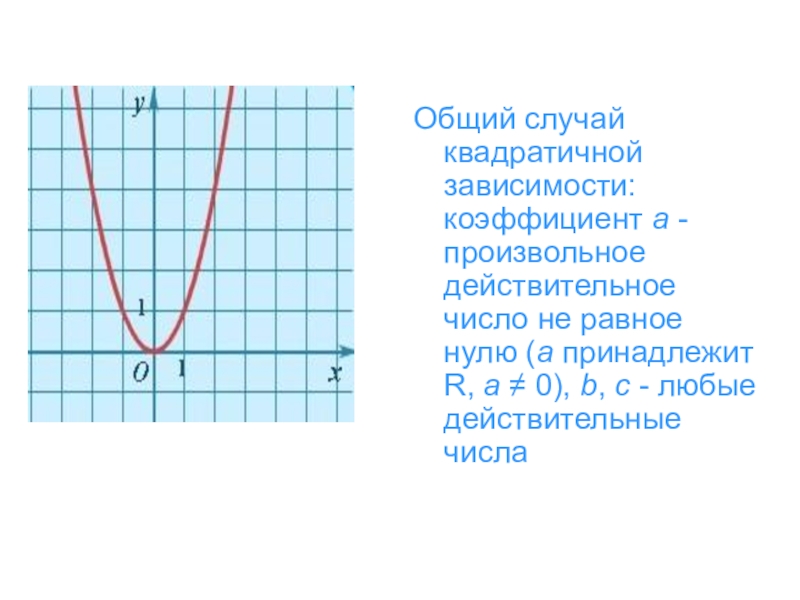
- 9. Общий случай квадратичной зависимости: коэффициент a - произвольное действительное
- 10. Степеннаяy = x3 Кубическая парабола
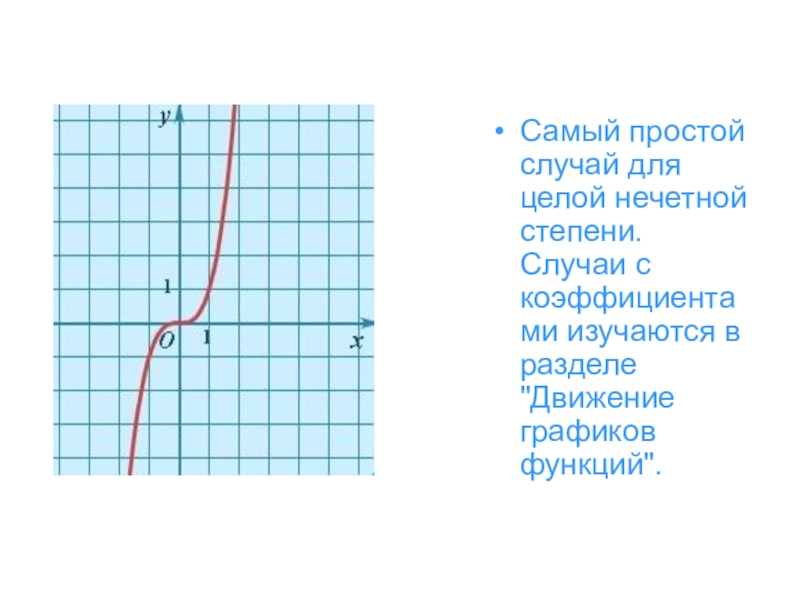
- 11. Самый простой случай для целой нечетной степени.
- 12. СтепеннаяГрафик функции y = √x y = x1/2
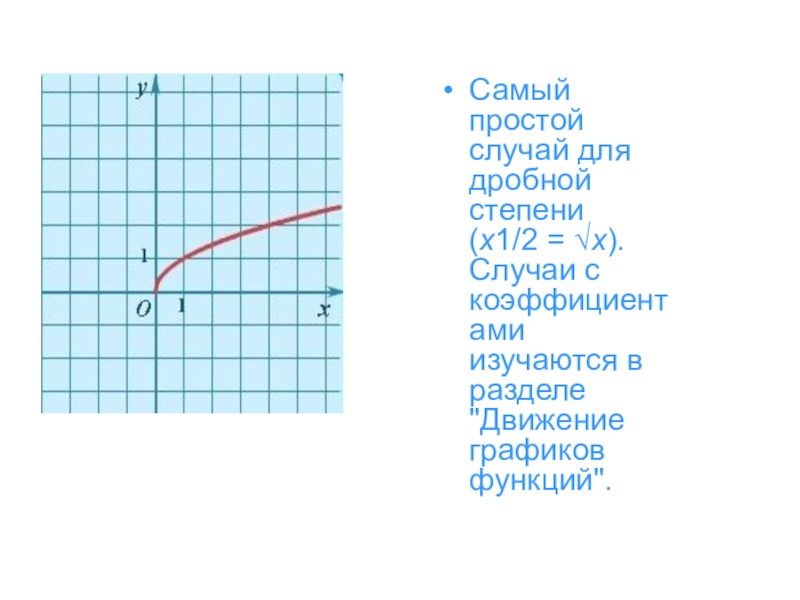
- 13. Самый простой случай для дробной степени (x1/2 =
- 14. Степеннаяy = k/x Гипербола
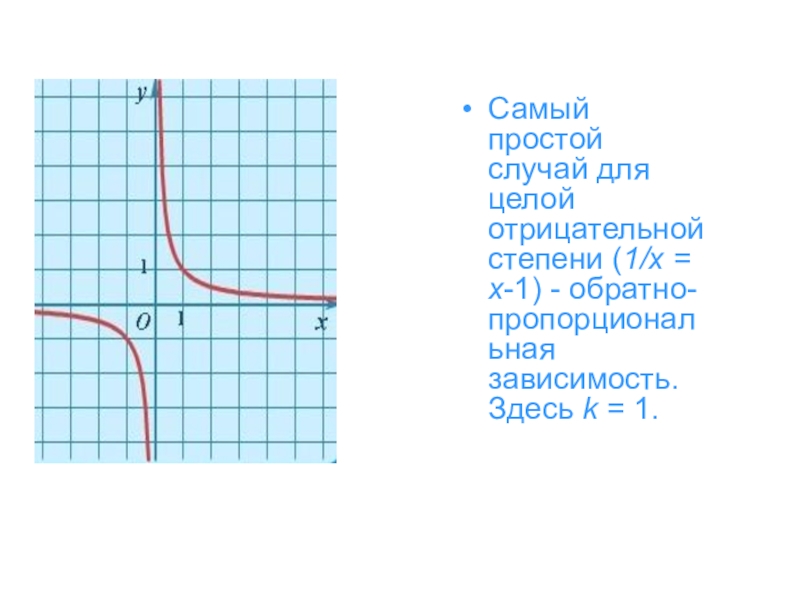
- 15. Самый простой случай для целой отрицательной степени (1/x = x-1) - обратно-пропорциональная зависимость. Здесь k = 1.
- 16. Показательнаяy = e(x) Экспонента
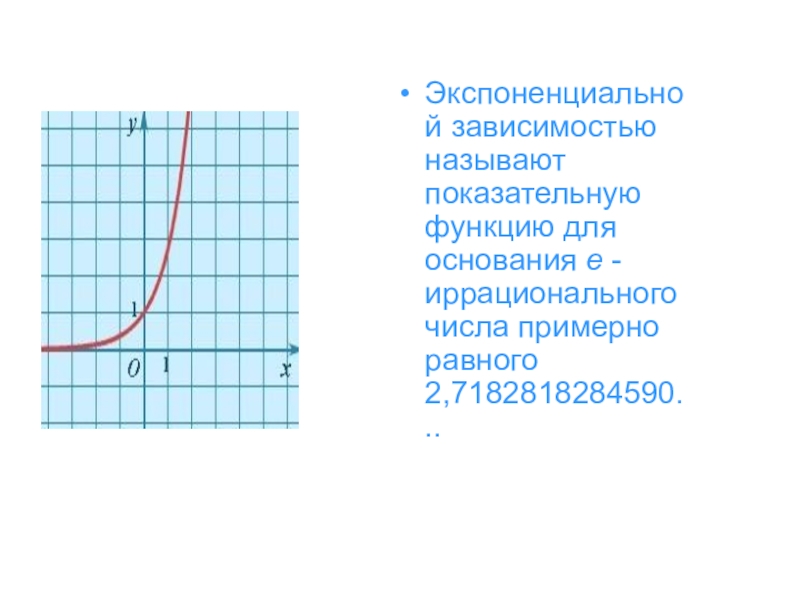
- 17. Экспоненциальной зависимостью называют показательную функцию для основания e - иррационального числа примерно равного 2,7182818284590...
- 18. Показательнаяy = a(x)График показательной функции
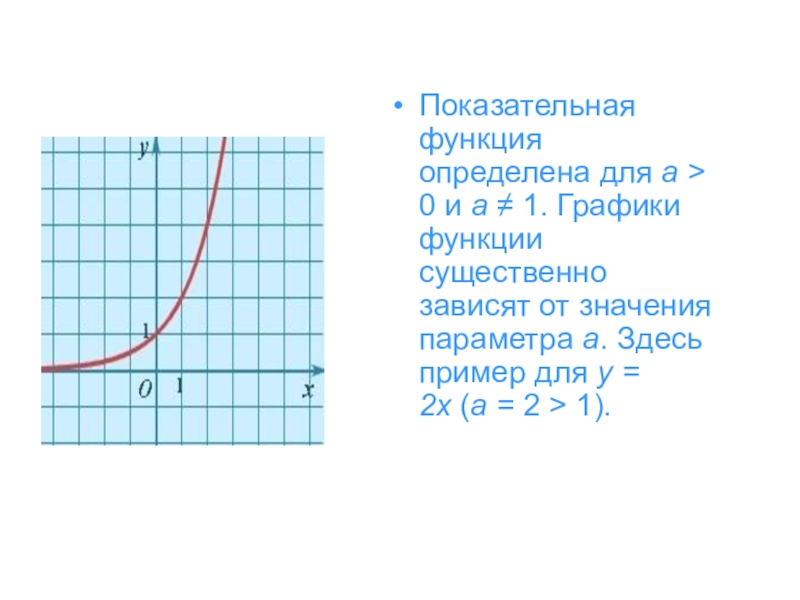
- 19. Показательная функция определена для a > 0 и a ≠ 1.
- 20. Показательнаяy = a(x) График показательной функции
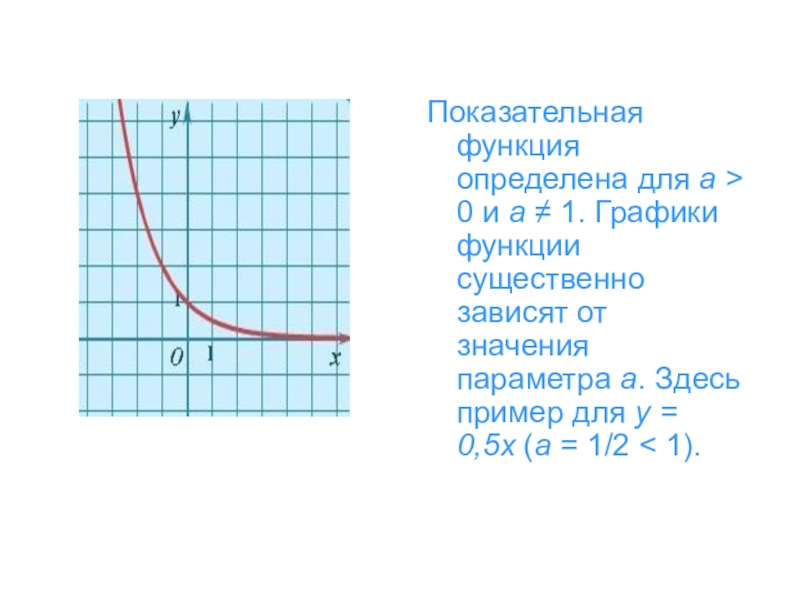
- 21. Показательная функция определена для a > 0 и a ≠ 1.
- 22. Логарифмическаяy = lnx График логарифмической функции
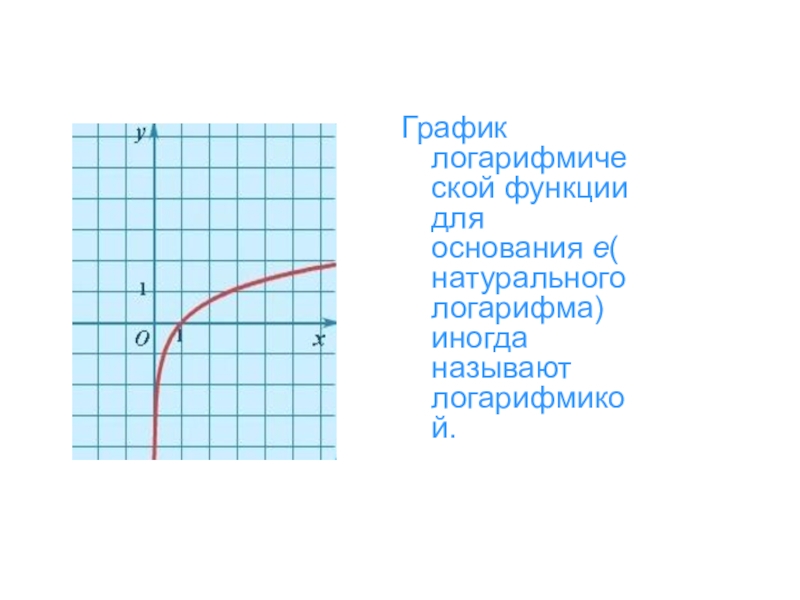
- 23. График логарифмической функции для основания e(натурального логарифма) иногда называют логарифмикой.
- 24. Логарифмическаяy = logax График логарифмической функции
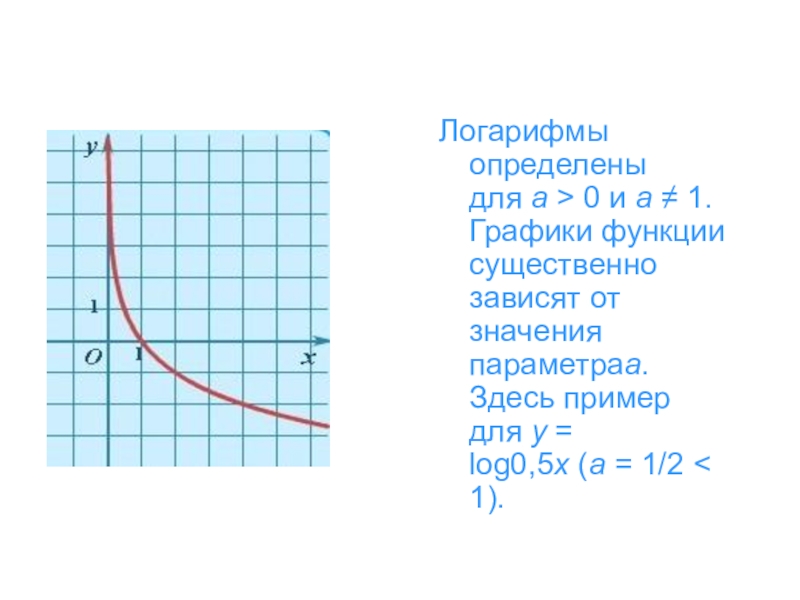
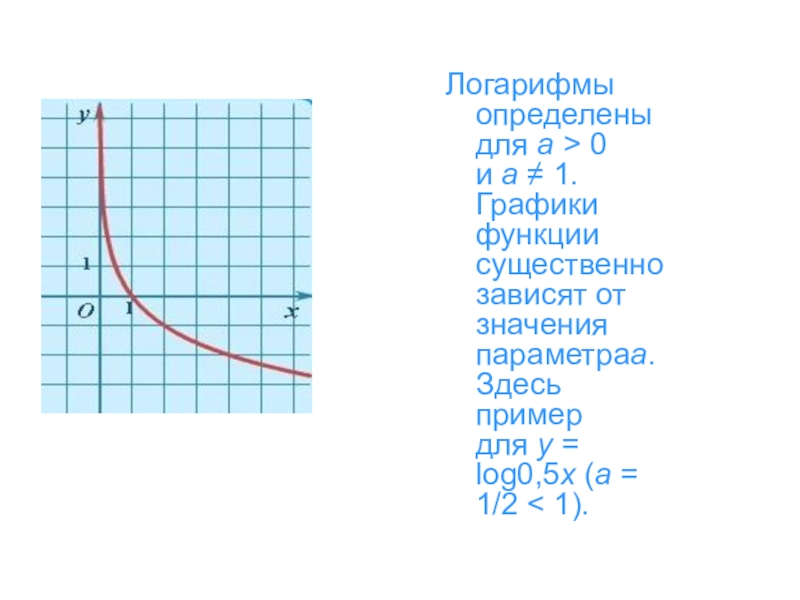
- 25. Логарифмы определены для a > 0 и a ≠ 1. Графики
- 26. Логарифмическаяy = logax График логарифмической функции
- 27. Логарифмы определены для a > 0 и a ≠ 1. Графики
- 28. Синусy = sinx Синусоида
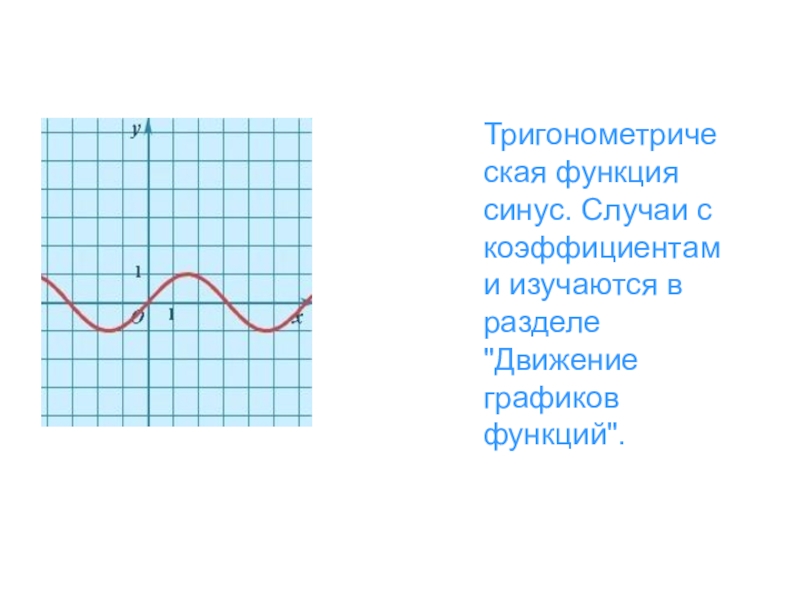
- 29. Тригонометрическая функция синус. Случаи с коэффициентами изучаются в разделе "Движение графиков функций".
- 30. Косинусy = cosx Косинусоида
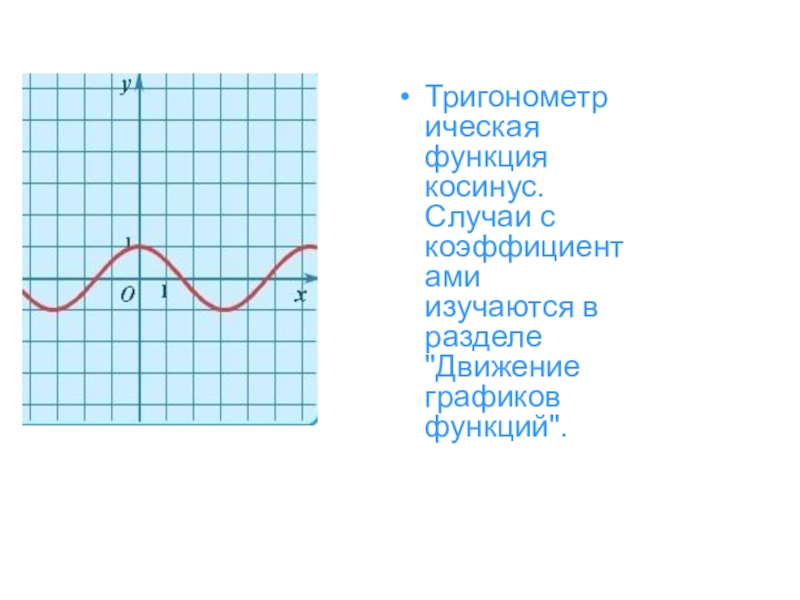
- 31. Тригонометрическая функция косинус. Случаи с коэффициентами изучаются в разделе "Движение графиков функций".
- 32. Тангенсy = tgx Тангенсоида
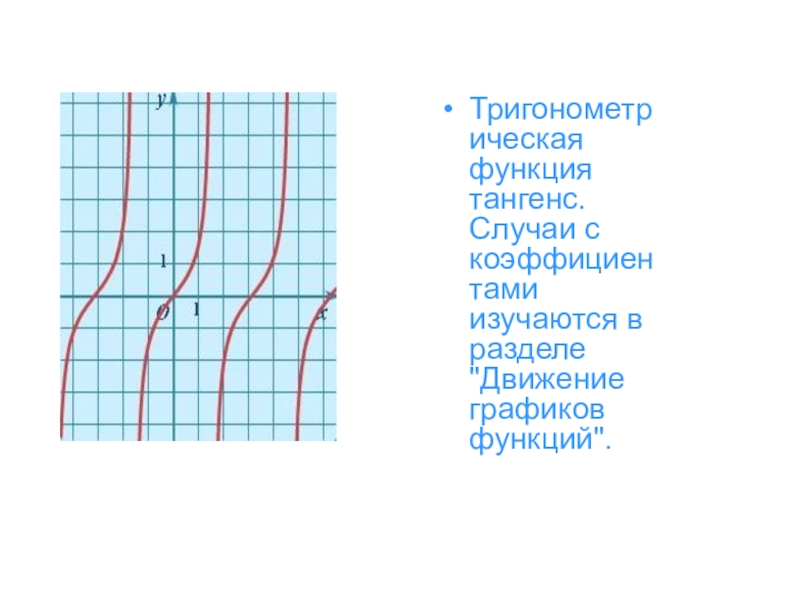
- 33. Тригонометрическая функция тангенс. Случаи с коэффициентами изучаются в разделе "Движение графиков функций".
- 34. Катангенсy = сtgx Котангенсоида
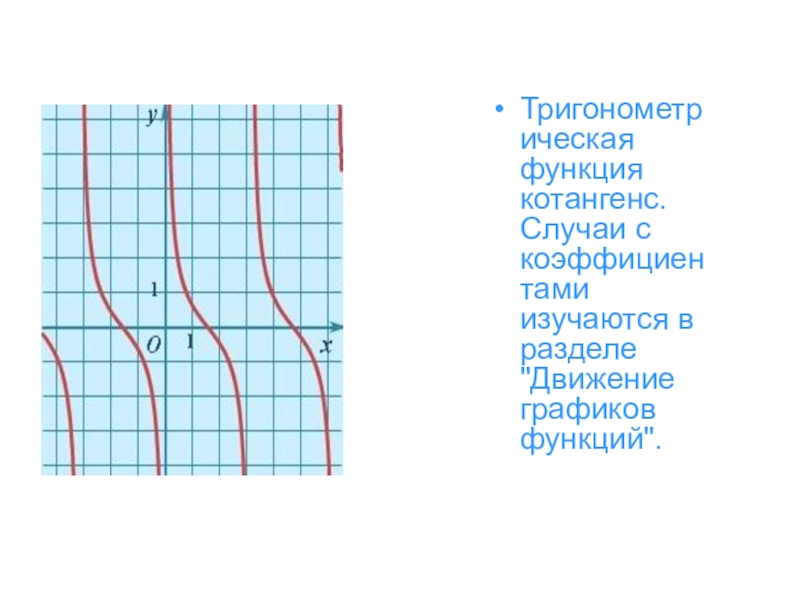
- 35. Тригонометрическая функция котангенс. Случаи с коэффициентами изучаются в разделе "Движение графиков функций".
- 36. Спасибо за внимание!!!Работу выполнила ученица 10 класса Бобик Александра Анатольевна
Линейнаяy=kxпрямая
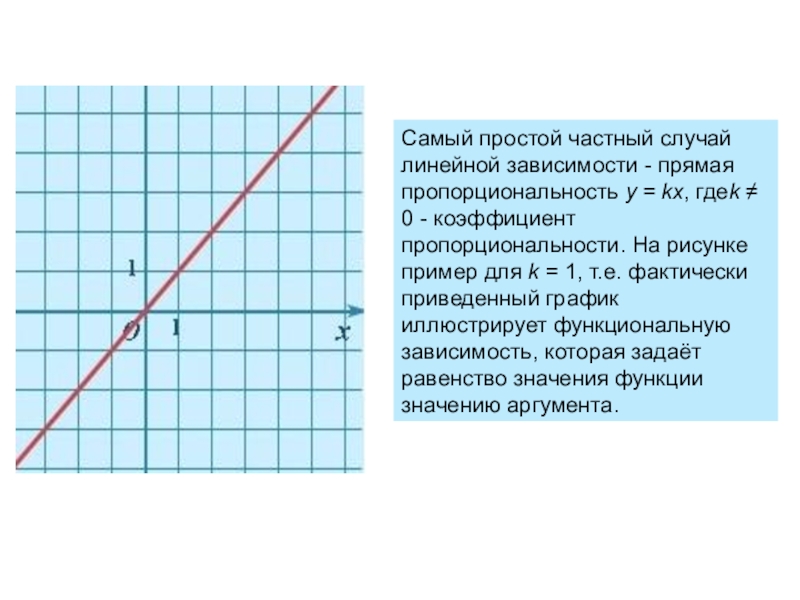
Слайд 3коэффициент пропорциональности. На рисунке пример для k = 1, т.е. фактически приведенный график
иллюстрирует функциональную зависимость, которая задаёт равенство значения функции значению аргумента.
Cамый простой частный случай линейной зависимости - прямая пропорциональность у = kx, гдеk ≠ 0 - коэффициент пропорциональности. На рисунке пример для k = 1, т.е. фактически приведенный график иллюстрирует функциональную зависимость, которая задаёт равенство значения функции значению аргумента.
Слайд 7Простейший случай квадратичной зависимости - симметричная парабола с вершиной в начале
координат.
Слайд 9Общий случай квадратичной зависимости: коэффициент a - произвольное действительное число не равное нулю
(a принадлежит R, a ≠ 0), b, c - любые действительные числа
Слайд 11Самый простой случай для целой нечетной степени. Случаи с коэффициентами изучаются
в разделе "Движение графиков функций".
Слайд 13Самый простой случай для дробной степени (x1/2 = √x). Случаи с коэффициентами
изучаются в разделе "Движение графиков функций".
Слайд 15Самый простой случай для целой отрицательной степени (1/x = x-1) -
обратно-пропорциональная зависимость. Здесь k = 1.
Слайд 17Экспоненциальной зависимостью называют показательную функцию для основания e - иррационального числа примерно равного
2,7182818284590...
Слайд 19Показательная функция определена для a > 0 и a ≠ 1. Графики функции существенно зависят
от значения параметра a. Здесь пример для y = 2x (a = 2 > 1).
Слайд 21Показательная функция определена для a > 0 и a ≠ 1. Графики функции существенно зависят
от значения параметра a. Здесь пример для y = 0,5x (a = 1/2 < 1).
Слайд 23График логарифмической функции для основания e(натурального логарифма) иногда называют логарифмикой.
Слайд 25Логарифмы определены для a > 0 и a ≠ 1. Графики функции существенно зависят от
значения параметраa. Здесь пример для y = log0,5x (a = 1/2 < 1).
Слайд 27Логарифмы определены для a > 0 и a ≠ 1. Графики функции существенно зависят от
значения параметраa. Здесь пример для y = log0,5x (a = 1/2 < 1).
Слайд 29
Тригонометрическая функция синус. Случаи с коэффициентами изучаются в разделе "Движение
графиков функций".
Слайд 31Тригонометрическая функция косинус. Случаи с коэффициентами изучаются в разделе "Движение графиков
функций".
Слайд 33Тригонометрическая функция тангенс. Случаи с коэффициентами изучаются в разделе "Движение графиков
функций".
Слайд 35Тригонометрическая функция котангенс. Случаи с коэффициентами изучаются в разделе "Движение графиков
функций".